问题描述
有一对兔子,从出生后的第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子,假设所有的兔子都不死,问30个月内每个月的兔子总对数为多少?
题目解析
兔子产子问题是一个有趣的古典数学问题,我们画一张表来找一下兔子数的规律,如表1.1所示。
| 月数 | 小兔子对数 | 中兔子对数 | 老兔子对数 | 兔子总对数 |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 1 | 0 | 1 | 2 |
| 4 | 1 | 1 | 1 | 3 |
| 5 | 2 | 1 | 2 | 5 |
| 6 | 3 | 2 | 3 | 8 |
| 7 | 5 | 3 | 5 | 13 |
我们可以发现,这个问题的繁殖模式符合斐波那契数列的递推规律:
- 第1、2个月只有一对兔子。
- 从第3个月开始,每个月的兔子总数等于前两个月兔子总数之和。因为新生的兔子对数等于两个月前的兔子对数。
算法设计
本题目是典型的迭代循环,即是一个不断用新值取代变量的旧值,然后由变量旧值递推出变量新值的过程。这种迭代与这些因素有关:初值、迭代公式和迭代次数。经过问题分析,算法可以描述为
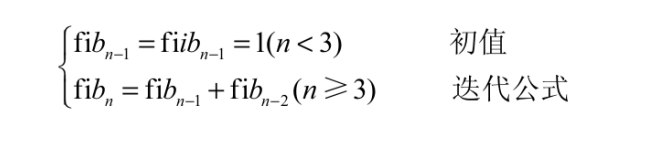
用Python语言来描述迭代公式即为fib=fib1+fib2,其中fib为当前新求出的兔子对数,fib1为前一个月的兔子对数,fib2为前两个月的兔子对数,然后为下一次迭代做准备,进行如下的赋值fib2=fib1,fib1=fib,要注意赋值的次序;迭代次数由循环变量控制,为所求的月数。
解题思路
- 定义斐波那契数列:兔子的数量符合斐波那契数列的递推关系。即:
F(n) = F(n-1) +F(n-2)(从第3个月开始)- 第1个月:
F(1)=1 对 - 第2个月:
F(2)=1 对
- 递推计算:从第3个月开始,每个月的兔子总数等于前两个月兔子数之和。
- 最终目标:我们需要计算30个月内每个月的兔子总对数。
代码实现
def rabbit_pairs(months):
if months <= 0:
return 0
elif months == 1 or months == 2:
return 1
# 初始化前两个数值
prev1, prev2 = 1, 1
# 从第三个月开始计算
for month in range(3, months + 1):
current = prev1 + prev2
prev1, prev2 = prev2, current
return current
# 计算30个月的兔子总对数
months = 30
total_rabbits = rabbit_pairs(months)
print(f"在第 {months} 个月,兔子的总对数为: {total_rabbits}")
解释:
- 递归关系:我们使用变量
prev1和prev2来存储前两个月份的兔子对数,然后通过递推计算当前月份的兔子总对数。
prev1存储的是前一个月的兔子对数。prev2存储的是当前月的兔子对数。- 每次更新这两个变量,直到计算出第30个月的兔子总对数。
- 递推过程:
- 初始时,第1、2个月的兔子总对数都为1对。
- 从第3个月开始,当前月的兔子总数等于前两个月兔子对数之和。
验证结果
运行上述代码后,得到30个月的兔子总对数为:
在第 30 个月,兔子的总对数为: 832040
总结:
这道题的繁殖模型符合斐波那契数列的递推关系。通过递推法,我们可以高效地计算每个月的兔子总对数,并快速得到30个月内兔子的数量。
