问题描述
编写用牛顿迭代法求方程根的函数。方程为ax3+bx2+cx+d=0,系数a、b、c、d由主函数输入,求x在1附近的一个实根。求出根后,由主函数输出。牛顿迭代法的公式

设迭代到|x-x0| ≤10-5时结束。
问题分析
牛顿迭代法是取x0之后,在这个基础上找到比x0更接近的方程根,一步一步迭代,从而找到更接近方程根的近似根。
设r是f(x)=0的根,选取x0作为r的初始近似值,过点(x0 ,f(x0))做曲线y=f(x)的切线L,L的方程为y=f(x0)+f'(x0)(x-x0),求出L与x轴交点的横坐标x1=x0-f(x0 )/f'(x0),称x1为r的一次近似值;过点(x1,f(x2))做曲线y=f(x)的切线,并求出该切线与x轴交点的横坐标x2=x1-f(x1)/f'(x1),称x2为r的二次近似值;重复以上过程,得到r的近似值xn 。上述过程即为牛顿迭代法的求解过程。
算法设计
程序流程分析:
- 在1附近找任一实数作为
x0的初值,我们取1.5,即x0=1.5。 - 用初值
x0代入方程中计算此时的f(x0 )及f'(x0 );程序中用变量f描述方程的值,用fd描述方程求导之后的值。 - 计算增量
h=f/fd。 - 计算下一个
x,x=x0-h。 - 用新产生的
x替换原来的x0,为下一次迭代做好准备。 - 若
|x-x0|>=1e-5,则转到步骤(3)继续执行,否则转到步骤(7)。 - 所求x就是方程
ax3+bx2+cx+d=0的根,将其输出。
确定程序框架
该程序的主体结构如下:
if __name__ == '__main__':
# 输入方程的系数
# 用牛顿迭代法求方程的根
# 输出所求方程的根
程序流程图如下图所示。
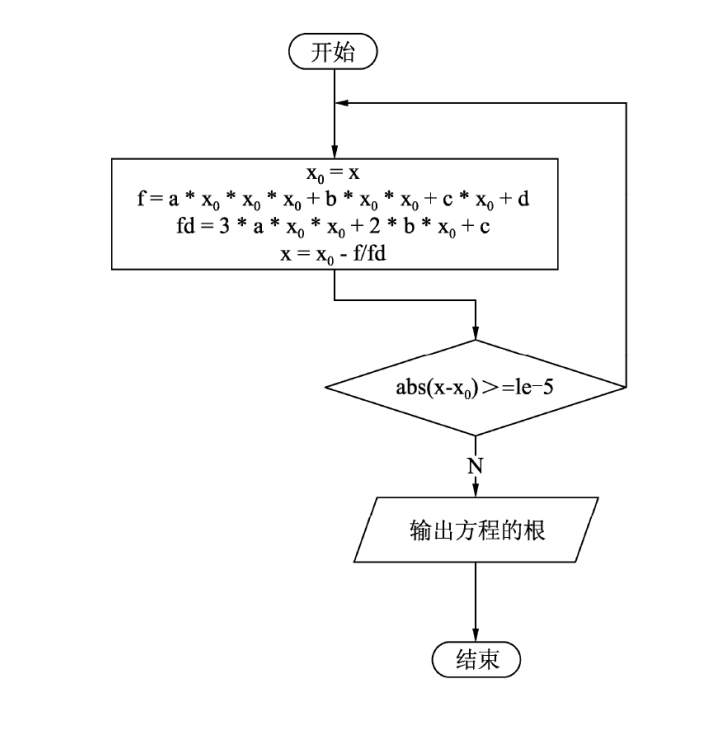
迭代法求方程根
编写程序时要注意的一点是判定|x-x0|>=1e-5,许多初学者认为判定条件应该是|x-x0|<1e-5,从牛顿迭代法的原理可以看出,迭代的实质就是越来越接近方程根的精确值,最初给x0
所赋初值与根的精确值是相差很多了,正是因为这个我们才需要不断地进行迭代,也就是程序中循环体的功能。在经过一番迭代之后所求得的值之间的差别也越来越小,直到求得的某两个值的差的绝对值在某个范围之内时便可结束迭代。若我们把判定条件改为|x-x0|<1e-5,则第一次的判断结果必为假,这样我们就不能进入循环体再次执行。希望初学者对于本类题目条件的判定要多加注意。
定义solution()函数求方程的根。solution()函数的代码如下:
#函数功能是用牛顿迭代法求方程的根
def solution(a, b, c, d):
x = 1.5
x0 = x # 用所求得的x的值代替x0原来的值
# f用来描述方程的值,fd用来描述方程求导之后的值
f = a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d
fd = 3 * a * x0 * x0 + 2 * b * x0 + c
h = f / fd
x = x0 - h # 求得更接近方程根的x的值
while abs(x - x0) >= 1e-5:
x0 = x
f = a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d
fd = 3 * a * x0 * x0 + 2 * b * x0 + c
h = f / fd
x = x0 - h # 求得更接近方程根的x的值
return x
完整的程序
根据上面的分析,编写程序如下:
# 函数功能是用牛顿迭代法求方程的根
def solution(a, b, c, d):
x = 1.5
x0 = x # 用所求得的x值代替x0原来的值
# f用来描述方程的值,fd用来描述方程求导之后的值
f = a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d
fd = 3 * a * x0 * x0 + 2 * b * x0 + c
h = f / fd
x = x0 - h # 求得更接近方程根的x值
while abs(x - x0) >= 1e-5:
x0 = x
f = a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d
fd = 3 * a * x0 * x0 + 2 * b * x0 + c
h = f / fd
x = x0 - h # 求得更接近方程根的x值
return x
if __name__ == '__main__':
print("请输入方程的系数:")
# a,b,c,d代表所求方程的系数
a, b, c, d = map(float, input().split())
print("方程的参数为:" , a, b, c, d)
# x用来记录求得的方程根
x = solution(a, b, c, d)
print("所求方程的根为x=%.6f"% x)
运行结果
在VScode下运行程序,结果如下图所示。

